[C] 이진 탐색 트리 (Binary Search Tree) 개념 및 구현
- -
개념
각각의 노드가 최대 두 개의 자식 노드(왼쪽 자식, 오른쪽 자식)를 가지고 있는 이진 트리 구조다.
데이터를 삽입할 때, 각각의 노드와 비교하며 삽입할 데이터가 노드의 데이터보다 작을 시 왼쪽 자식으로,
클 시 오른쪽 자식으로 내려가며 비어있는 곳까지 내려가 삽입된다.
특징
1. 트리에서 데이터를 검색할 때 이진 탐색 알고리즘과 동일한 시간 복잡도의 성능을 가진다.
2. 중위 순회로 데이터들을 정렬된 상태로 순회할 수 있다.
3. 배열로도 구현이 가능하고, 연결 리스트로도 구현이 가능하다.
따라서 구현한 자료구조에 따라서 해당 자료구조의 특징을 갖는다.
4. 요소의 삽입, 삭제, 접근은 O(logN), 최악의 경우 O(N) 이다.
장점
1. 특정 데이터를 검색할 때 꽤나 빠른 편이다. O(logN)
2. 데이터를 삽입할 때 약간의 오버헤드를 가지지만, 중위 순회로 데이터들의 정렬된 상태를 볼 수 있기 때문에
데이터들이 정렬된 상태를 유지해야 한다면, 채택하기에 적합하다.
단점
1. 자가 균형(Self-balancing) 기능이 없다면, 데이터의 삽입이 한 쪽으로 치우쳐진 경우
기대했던 성능이 나오지 않을 수 있다.
(예를 들어 1, 2, 3, 4, 5를 차례대로 삽입 시, 트리의 깊이가 4가 되며 삽입, 삭제, 탐색이 O(N)이 된다.)
상세 설명

대충 이진 탐색 트리는 위와 같이 생겼다.
하지만 어떤 데이터를 먼저 삽입했느냐에 따라 아래처럼 트리의 모양이 달라지게 된다.

최악의 경우 일자로 길게 늘어선 모양이 나올 수도 있다.
따라서 실제로 사용할 경우에는 자가 균형 기능이 있는 트리를 사용하는 것이 바람직하다.
하지만 본 포스팅은 자가 균형(Self-balancing)이 없는 기본 이진 탐색 트리 기준이다.
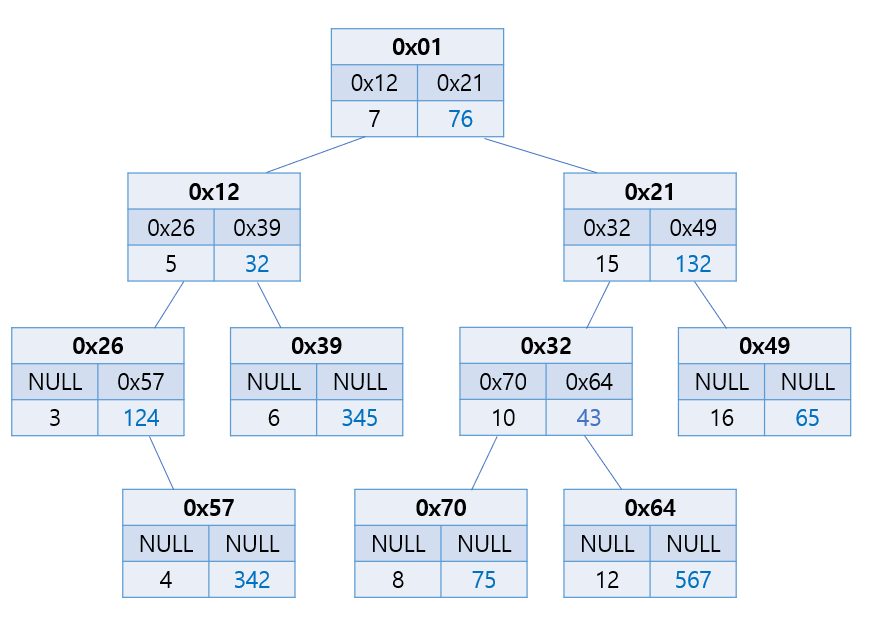
위의 단순했던 동그라미 모양의 노드는 사실 이렇게 생겼다.
왼쪽 자식 노드의 주소, 오른쪽 자식 노드의 주소, 데이터가 필요하다.
트리 구조에서의 데이터는 사진처럼 데이터가 키, 값의 쌍으로 많이 사용한다. 키를 가지고 찾으면 값이 나오는 구조다.
이 것들을 감싸고 있는 녀석도 하나 만들어 주면 편하다.

트리의 최상위 노드(Root)와 트리의 크기(Size)이다.
최상위 노드만 알고 있다면, 각 노드는 왼쪽 자식과 오른쪽 자식의 주소를 알고 있으니 연결 되어있는 셈이다.
삽입, 삭제, 탐색, 순회에 대한 자세한 설명은 구현 파트에서 설명하겠다.
구현
일단 본격적으로 들어가기 전에 필자는 키, 값 쌍으로 된 데이터를 다룰 것이기 때문에 이에 대한 코드부터 소개하겠다.
typedef struct pair
{
int key;
int value;
} pair;
pair* make_pair(int key, int value)
{
pair* new_pair = (pair*)malloc(sizeof(pair));
new_pair->key = key;
new_pair->value = value;
return new_pair;
}
C++의 STL의 pair를 참고하여 만든 pair 구조체다. key와 value를 감싸고 있다.
설명에 앞서 참고해야할 사항 몇 가지
우선 트리의 할당과 해제는 프로그래머에게 맡긴다.
따라서 트리는 이미 할당되어 있다는 가정을 한다.
또한 다음과 같은 사항은 코드의 가독성 문제 등으로 염려에 두지 않았다.
1. 함수의 트리(tree) 매개변수가 NULL pointer일 경우
2. malloc() 이 실패한 경우
3. free() 후 댕글링 포인터
4. size의 overflow
5. 재귀 함수로 인한 stack overflow
구조체
typedef struct node
{
struct node* lchild;
struct node* rchild;
pair* data;
} node;
typedef struct tree
{
node *root;
int size;
} tree;tree의 각 node들은 왼쪽 자식 노드의 주소와 오른쪽 자식 노드의 주소를 가지고 있고,
위에서 설명한 data를 가지고 있다.
tree는 최상위 노드인 root 노드의 주소만 가지고 있다.
초기화
void initialize(tree* tree)
{
tree->root = NULL;
tree->size = 0;
}tree의 할당은 프로그래머에게 맡기므로 NULL과 0으로 초기화만 시켜준다.
데이터 삽입
static node* recursion_insert(tree* tree, node* cur, pair* data)
{
if (cur == NULL)
{
node* new_node = (node*)malloc(sizeof(node));
new_node->lchild = NULL;
new_node->rchild = NULL;
new_node->data = data;
if (tree->size == 0)
tree->root = new_node;
++tree->size;
return new_node;
}
if (data->key > cur->data->key)
cur->rchild = recursion_insert(tree, cur->rchild, data);
else if (data->key < cur->data->key)
cur->lchild = recursion_insert(tree, cur->lchild, data);
else
free(data);
return cur;
}
void insert(tree* tree, pair* data)
{
recursion_insert(tree, tree->root, data);
}필자는 이진 탐색 트리의 구현에 재귀함수를 본격적으로 사용하였다.
stack overflow 위험 때문에 재귀함수를 선호하지는 않지만, 트리 구현에는 보통 쓰이기도 하고
이 참에 재귀적 사고를 더 기르기 위해 사용하게 되었다.
굳이 호출 함수와 재귀 함수를 나눠둔 이유는, 함수 사용에 대한 편의성 때문이다.
삽입하려는 key와 현재 순회중인 노드의 key를 비교하여,
삽입하려는 key가 작으면 왼쪽 자식으로, 크면 오른쪽 자식으로 더욱 깊이 들어가며 탐색한다.
만약, 이미 해당 key가 존재하면, 더이상 들어가지 않으며 삽입하려는 데이터를 free해준다.
재귀의 중단점은 계속 들어가며 탐색하던 노드가 NULL일 경우인데,
이 때 새 노드를 할당해주고, root와 size에 대한 작업을 마친 후 새 노드를 반환해준다.
반환을 받은 곳에서 바로 해당 방향의 자식 주소에 복사해주며 종료.
나머지는 cur 노드를 반환하기 때문에 변동이 없다.
데이터 탐색
pair* find(tree* tree, int key)
{
node* cur = tree->root;
while (cur != NULL)
{
if (key > cur->data->key)
cur = cur->rchild;
else if (key < cur->data->key)
cur = cur->lchild;
else
return cur->data;
}
return NULL;
}데이터를 삽입할 때와 똑같은 방식으로 순회해준다.
딱히 재귀 함수가 필요 없기 떄문에 반복문으로 처리했다.
순회하면서 찾았으면 해당 데이터를 반환해주고, 못 찾았으면 NULL pointer를 반환한다.
데이터 삭제
static node* get_similar_node(node* cur)
{
cur = cur->lchild;
while (cur->rchild != NULL)
cur = cur->rchild;
return cur;
}
static node* recursion_erase(tree* tree, node* cur, int key)
{
if (cur == NULL)
return NULL;
if (key == cur->data->key)
{
if (cur->lchild == NULL || cur->rchild == NULL)
{
node* temp;
if (cur->lchild == NULL)
temp = cur->rchild;
else
temp = cur->lchild;
if (cur == tree->root)
tree->root = temp;
--tree->size;
free(cur->data);
free(cur);
return temp;
}
else
{
node* next = get_similar_node(cur);
free(cur->data);
cur->data = make_pair(next->data->key, next->data->value);
cur->lchild = recursion_erase(tree, cur->lchild, next->data->key);
}
}
else if (key > cur->data->key)
cur->rchild = recursion_erase(tree, cur->rchild, key);
else if (key < cur->data->key)
cur->lchild = recursion_erase(tree, cur->lchild, key);
return cur;
}
void erase(tree* tree, int key)
{
recursion_erase(tree, tree->root, key);
}이진 탐색 트리에서는 삭제하려는 데이터의 자식이 몇개냐에 따라 달라지므로 꽤나 복잡하다.
중간에 있는 데이터를 삭제하더라도, 이진 탐색 트리의 구조는 유지되어야 하기 때문이다.
먼저, 인자로 받은 key를 통해 트리에서 삭제할 노드를 탐색한다. 탐색 방법은 지금까지 했던 방식과 똑같다.
탐색이 완료된 후에는 아래와 같은 과정을 거친다.
1. 삭제하려는 노드의 자식이 없을 경우


사진과 같이 없으면 그냥 삭제해주고 끝난다.
2. 삭제하려는 노드의 자식이 1개 있을 경우

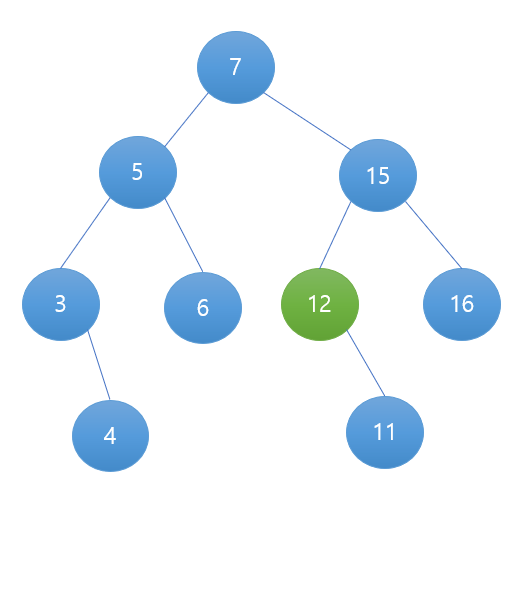
사진과 같이 기존 노드를 지워주고 기존 노드의 부모 노드에 기존 노드의 자식 노드를 연결시켜주면 끝이다.
2. 삭제하려는 노드의 자식이 2개 모두 있을 경우

15를 지운다고 가정해보자.
먼저 15와 가장 유사한 노드를 찾아야한다.
1. 이는 15의 왼쪽 서브트리에 존재하는 제일 오른쪽에 있는 자식노드,
2. 15의 오른쪽 서브트리에 존재하는 제일 왼쪽에 있는 자식 노드 중 하나이다.
취향껏 골라도 되고, 둘 중 더욱 비슷한 녀석을 골라도 된다.
필자는 1번으로 결정했고, 이는 사진의 12와 같다.
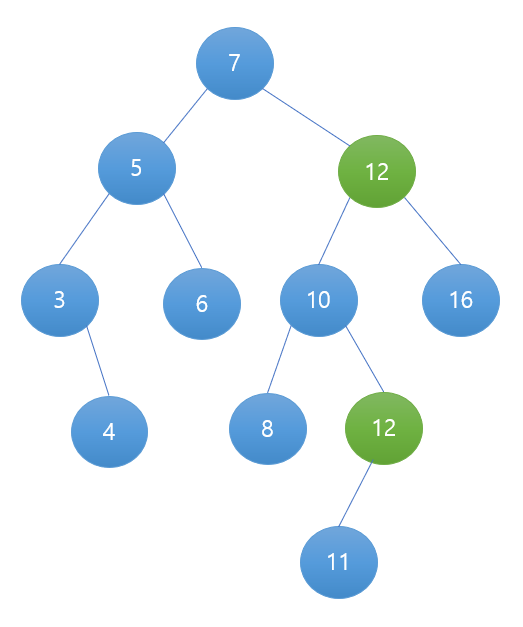
다 골랐으면 고른 노드를 삭제할 노드에 옮겨주는 작업을 해야한다.
이런 작업을 통해 이진 탐색 트리의 구조를 유지할 수 있다.
15로 옮겨주었으면 기존의 12는 삭제해주어야 한다.

타겟이 바뀌었다. 이번엔 12가 삭제할 노드가 되는 것이다.
12의 자식은 11 하나 뿐이기 때문에 12를 지우고 11을 10과 연결해주기만 하면 된다.

이렇게 15라는 데이터 삭제가 완료되었다.
만약 12의 자식이 더 있다면 무한하게 재귀로 반복할 것 같지만,
제일 유사한 값의 노드를 찾는 로직에서 이미 해당 노드는 무조건 자식이 없거나 하나이다.
(12의 오른쪽 자식이 있었다면, 다음 타겟은 12가 아니라 12의 오른쪽 자식이 될 것이었다.)
따라서 데이터의 삭제는 최대 두 번 일어나게 된다.
재귀의 중단점은 찾지 못했거나 (NULL pointer) 찾았을 경우인데,
찾았을 경우 해당 노드의 자식 개수에 따라 더 재귀를 들어갈 것인지 말지가 결정된다.
자식이 2개라면, 타겟이 바뀌고 기존의 15 삭제에 대한 로직은 끝난 거라고 보면 되므로 data를 옮겨 준 뒤
바뀐 타겟에 대한 재귀를 추가적으로 수행하는 것이다.
모든 데이터 삭제
static void recursion_clear(node* cur)
{
if (cur == NULL)
return ;
recursion_clear(cur->lchild);
recursion_clear(cur->rchild);
free(cur->data);
free(cur);
}
void clear(tree* tree)
{
recursion_clear(tree->root);
initialize(tree);
}모든 데이터 삭제를 위해 후위 순회를 해야한다.
전위 순회는 자신, 왼쪽 자식, 오른쪽 자식 순으로 순회하는 것이며,
중위 순회는 왼쪽 자식, 자신, 오른쪽 자식 순으로 순회하는 것이고,
후위 순회는 왼족 자식, 오른쪽 자식, 자신 순으로 순회하는 것이다.
전, 중, 후는 자신을 가리킨다고 생각하면 외우기 편하다.
재귀의 중단점은 NULL pointer까지 내려갔을 경우이고, 이후 나오면서 데이터와 노드를 free,
이제 왼쪽 자식은 끝까지 갔으니 오른쪽 자식을 순회하고 나오면서 free,
자신의 서브트리를 모두 free하고 나서야 자신을 free해야한다.
데이터 정렬된 상태로 순회
void recursion_print(node* cur)
{
if (cur == NULL)
return ;
recursion_print(cur->lchild);
printf("(%d:%d) ", cur->data->key, cur->data->value);
recursion_print(cur->rchild);
}
void print(tree* tree)
{
printf("[size:%d] ", tree->size);
recursion_print(tree->root);
printf("\n");
}이진 탐색 트리의 또다른 장점, 정렬이다.
이는 위에서 말한 것처럼 중위 순회만 하면 바로 가능하다.
정렬된 상태에서 무엇이든 할 수 있지만 필자는 출력을 하는 함수로 구현해보았다.
중위 순회를 진행하며 자신일 때 출력해주면 끝이다.
테스트

리눅스 환경에서 여러 컴파일 옵션을 줘서 테스트했고
메모리 누수 포함 에러가 (아직은) 없는 것을 확인했다.
↓ 테스트 코드 확인하기
#include "BinarySearchTree.h"
int main()
{
tree tree;
printf("----- initialize -----\n");
initialize(&tree);
print(&tree);
printf("\n----- insert -----\n");
insert(&tree, make_pair(7, 0));
print(&tree);
insert(&tree, make_pair(5, 0));
print(&tree);
insert(&tree, make_pair(15, 0));
print(&tree);
insert(&tree, make_pair(3, 0));
print(&tree);
insert(&tree, make_pair(6, 0));
print(&tree);
insert(&tree, make_pair(10, 0));
print(&tree);
insert(&tree, make_pair(16, 0));
print(&tree);
insert(&tree, make_pair(4, 0));
print(&tree);
insert(&tree, make_pair(8, 0));
print(&tree);
insert(&tree, make_pair(12, 0));
print(&tree);
insert(&tree, make_pair(11, 0));
print(&tree);
printf("\n----- find -----\n");
printf("%p\n", find(&tree, 16));
printf("%p\n", find(&tree, 4));
printf("%p\n", find(&tree, 7));
printf("%p\n", find(&tree, 20));
printf("\n----- erase -----\n");
erase(&tree, 15);
print(&tree);
erase(&tree, 12);
print(&tree);
erase(&tree, 11);
print(&tree);
erase(&tree, 10);
print(&tree);
erase(&tree, 8);
print(&tree);
erase(&tree, 16);
print(&tree);
erase(&tree, 7);
print(&tree);
erase(&tree, 5);
print(&tree);
erase(&tree, 3);
print(&tree);
printf("\n----- clear -----\n");
clear(&tree);
print(&tree);
printf("\n----- edge cases -----\n");
clear(&tree); // double clear
print(&tree);
insert(&tree, make_pair(1, 1));
print(&tree);
insert(&tree, make_pair(1, 5)); // insert duplicate key
print(&tree);
erase(&tree, 5); // key not found when erase
print(&tree);
erase(&tree, 1);
print(&tree);
erase(&tree, 1); // erase at empty tree
print(&tree);
}
↓ 테스트 코드의 삭제 로직 (그림)
주황색 : 현재 타겟
초록색 : 현재 타겟과 바꿀 데이터










마무리
BST(이진 탐색 트리) 구현은 설계에 대한 고민이 많았다.
웬만하면 재귀 함수의 사용을 피하고 싶었지만 그렇다고 stack을 이용해서 구현하는 것은 더욱 복잡했다.
재귀로 BST에 대한 구현 능력을 다졌으니 다음에는 stack으로 구현해보고 싶은 생각이 든다.
또한 자가 균형 기능의 BST는 다음 C++ STL 구현 파트에서 진행해보도록 하겠다.
마지막으로 전체 코드
https://github.com/SikPang/DataStructures/tree/main/C_BinarySearchTree
GitHub - SikPang/DataStructures
Contribute to SikPang/DataStructures development by creating an account on GitHub.
github.com
개인 공부용 포스팅인 점을 참고하시고, 잘못된 부분이 있다면 댓글로 남겨주시면 감사드리겠습니다.
'Data Structure > C' 카테고리의 다른 글
| [C] 해시 테이블 (Hash Table) 개념 및 구현 (0) | 2023.03.30 |
|---|---|
| [C] 덱 (Deque) 개념 및 원형 덱 구현 (2) | 2023.03.23 |
| [C] 동적 배열 (Dynamic Array) 개념 및 구현 (0) | 2023.03.22 |
| [C] 연결 리스트 (Linked List) 개념 및 구현 (1) | 2023.03.21 |
소중한 공감 감사합니다